Obsah
Jeste pred prechodem na vlastni vypocet je tu maly benchmark inicializacniho
vypoctu na 11 strojich:
Metoda \ Pocet procesu
|
3
|
5
|
6
|
8
|
10
|
11
|
Metoda 2
|
842 s
|
701 s
|
287 s
|
862 s
|
350 s
|
331 s
|
Metoda 3
|
658 s
|
459 s
|
228 s
|
277 s
|
179 s
|
168 s
|
Metoda 2 zcela dle ocekavani neni schopna zajistit ani vzdalene linearni
narust vykonu a dokonce vykazuje lepsi vysledky na 6 procesech nez pri 11!!!
Jeste propastnejsi je rozdil mezi pouzitim 6 a 8 pocitacu - prestoze pouzijeme
k vypoctu o dva pocitace vic, tak vypocetni doba se prodlouzi temer na
trojnasobek. Mensi ztratu vykonu je mozno v teto situaci pozorovat i pri
treti metode. Duvodem je, ze pri rozdeleni na 6 procesu mu to vyjde hezky
na dvojice, zatimco pri 8 uz se vic prekryvaji a musi vic cekat. Podstatnym
vysledkem mereni je skutecnost temer linearniho rustu vykonu u metody 3,
ktera se timto stava nas lidr do budoucna.
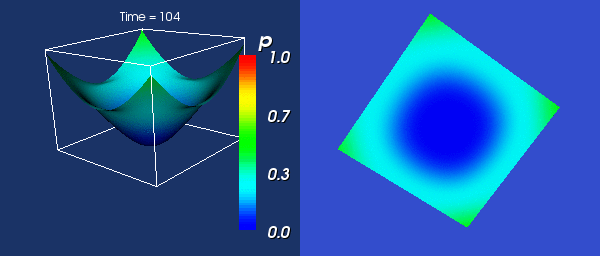
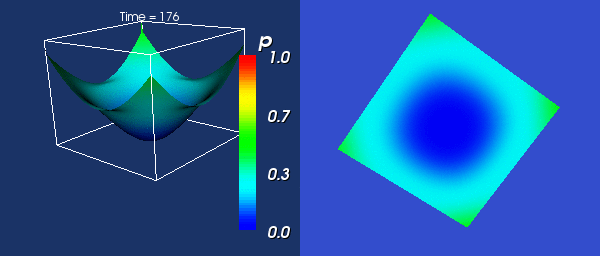
Vyvoj v case
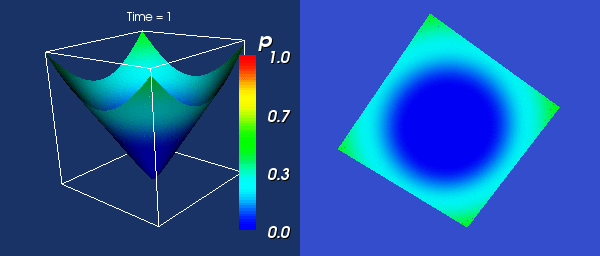
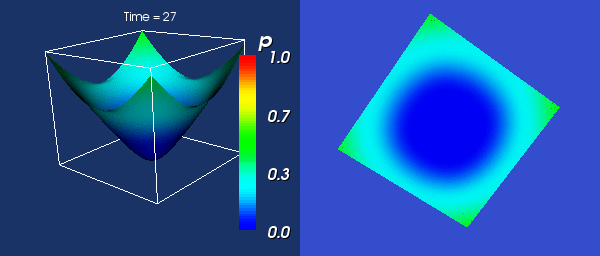
Pochopitelne jsem zacal vypoctem zadaneho evolucniho vzorce. Zadny
vetsi problem se snad ani nemohl vyskytnout, a tak je vzoreckova cast
jiz napsana. Zacal jsem vypoctem vyhradne urcenym pro narrow band - tedy
s vyuzitim cache bloku (a proto nejde pouzit pro normalni bodovy vypocet).
Resp. pujde pouzit, ale bude se muset cely prepsat na jine promenne. Bude
tu celkem velka redundance kodu, proti ktere jsem dosud velice uspesne
bojoval. :-( Smula. Snad me jeste neco napadne jak zachovat rychlost a nemuset
cele bloky kodu psat kopi-end-pejst stylem.
Duvod, proc tu nejsou zatim vysledky je jednoduchy - narazil jsem
na problem s postupem. V pripade, za se krivka bude v jedne vzdalene casti
blizit k jine casti zhruba rovnobezne a ve vzdalenosti pul naseho pokryvajiciho
bloku (tufiz na jeho hrane), tak program bude velmi nepresny eventualne
nebude schopen zjistit, kdy reinicializovat.. V jednom procesu tam bude
sice presna hodnota, ale druhy bude na stejnych polich pocitat uplne zcestne.
Reseni:
- Synchronizovat procesy na urovni mensich pokryvajicih bloku.
V podstate na bazi, ze se body na krajich bloku nebudou aproximovat,
ale budou se hledat procesy, ktere tento bod maji. Hezke, ale pravdepodobne
extremne narocne na vypocet (pomerne i na implementaci). Na teto myslence
jsem jiz zacal pracovat...
- Zmenit pokryvaci strategii. Zacit stejne jako nyni, jen neskoncit
po prvnim pruchodu a zkusit najit dalsi body, ktere patri do naseho ramce.
Je podstatne jednodussi. Neresi ale problem s aproximaci na krajich bloku.
Do dalsiho vyvoje se pustim az s trochu rozmyslenou strategii (tzn.
po vikendu), protoze se mi to u predchoziho programovani zatim vzdy velice
vyplatilo. O cemz svedci i temer nulova redundance kodu pro pripady NarrowBand
a Bodoveho pocitani primo na matici.
Informace o clusteru: Petr je (snad az prilis :-) ) aktivni,
a tak je cluster odladen pro normalni pouziti. Zatim nefunguje jednoduche
bootovani bez potreby nastavovani SSH-agenta. To ale nevadi, protoze
s touto moznosti jsem ani nepocital a lze jej spustit i tak s jen o neco
vetsi praci. Kamilovi jsem v rychlokurzu vysvetlil praci na LAM implementaci
MPI a domluvili si prvni spolecny zazeh, predbezne na ctvrtek cca. 14.11.
vecer. To jen, abysme zbytecne nepousteli pocitace pres noc jen pro jednoho.
Zaroven je jiz odladeny skriptik na detekci bezicich pocitacu i samotne
spusteni clusteru (ten se zprovoznenim bezagentoveho zpusobu stane zbytecnym).
Protoze mi bylo tak trochu hloupe Petrovi stale pridelavat praci jeste
s clusterem, tak jsem se s nim domluvil na pomoci pri sprave.