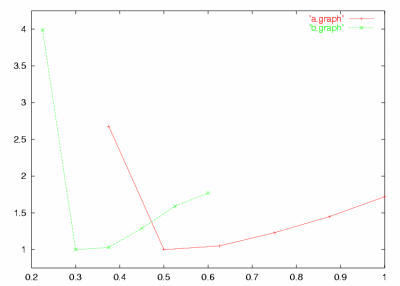
Cervena - sit s krokem 0.025, Zelena 0.015. Vidime
docela ocekavanou zavislost - prilis uzky pas zpusobuje caste
reinicializace a vypocet je relativne pomaly. S rozsirovanim pasu cas
velice rychle klesa a pote uz relativne pomalu roste. Nelze jednoznacne
rici, jak siroky pas vzit, protoze je to velice zavisle na konkretnim
vypoctu, ale zhruba muzeme doporucit udelat pas radeji sirsi. V
paramatrech pasu je ale prilis promennych...
Opetovne se take muzeme podivati, jak se meni chyba v zavislosti na sirce kroku. Z predchozich mereni vime, ze chyba je mnohem vice zavisla na "vzdalenosti od kraje" nez na vlastni sirce. Takze overme... Jsme liny delat graf, takze opet tabulka. :-)
Asi by bylo nejlepsi tyto vysledky zaprit, ale... Nutno podotknout, ze jsme to moc neoverili - naopak ted mam pocit, ze lze docela podstatne vylepsit rozsirenim pasu. Hlavne skok 25->30 u hrubsiho kroku je velice citelny...
Konecne mam dostatek casu udelat komplexnejsi test nastaveni uzkeho pasu - zvolil jsem zavislost na dvou vybranych parametrech, ktere jsou podle me nejdulezitejsi a nejvice ovlivnuji vysledek. Jsou to sirka a prisnost reinicializce (presneji, kam postavit detekcni miny pro reinicializaci). A protoze stale nejde poznat, co to tedy je, tak vysvetlim jak je to implementovane - prisnost znaci procentualni vzdalenost min od kraje. Tzn. ze 50% znamena, ze uz bude jen velice malo min na krajich. Nejdrive se podivame na chybu. Pro presnost podotykam, ze krok je 0.01, kde plna domena dosahuje chyby 9.05e-5 za XXX vterin (simulace probehly na starem clusteru).
Chyba
<3aniz7>
Doba vypoctu/ / pocet reinicializaci
<3aniz7>
A nakonec jen napocitani ucinnosti paralelizace na plne domene na SP. Na kroku 0.01 a casovem 7.8e-6.
<3aniz8>
Bohuzel na jednom uzlu uz to nebylo mozne spocitat z duvodu omezeni doby vypoctu na 2dny. :-(
Ponekud zarazejici vysledek si vysvetluji tim, ze jsou to vsechno dualni masiny, kazde dva procesy tedy maji jen jeden komunikacni kanal. Dusledkem je, ze komunikace s ostatnimi procesy trva zhruba 2x tak dlouho, nez by melo - coz jsme presne pozorovali.
Opetovne se take muzeme podivati, jak se meni chyba v zavislosti na sirce kroku. Z predchozich mereni vime, ze chyba je mnohem vice zavisla na "vzdalenosti od kraje" nez na vlastni sirce. Takze overme... Jsme liny delat graf, takze opet tabulka. :-)
| Krok \ Sirka pasu v bodech (!!) |
15 |
20 |
25 |
30 |
35 |
40 |
| 0.025 |
7.3e-2 |
6.5e-2 |
3.4e-2 |
1.4e-2 |
1.2e-3 |
2.2e-3 |
| 0.015 |
1.13e-1 |
9.3e-2 |
6.1e-2 |
3.8e-2 |
1.9e-2 |
5.8e-3 |
Asi by bylo nejlepsi tyto vysledky zaprit, ale... Nutno podotknout, ze jsme to moc neoverili - naopak ted mam pocit, ze lze docela podstatne vylepsit rozsirenim pasu. Hlavne skok 25->30 u hrubsiho kroku je velice citelny...
Konecne mam dostatek casu udelat komplexnejsi test nastaveni uzkeho pasu - zvolil jsem zavislost na dvou vybranych parametrech, ktere jsou podle me nejdulezitejsi a nejvice ovlivnuji vysledek. Jsou to sirka a prisnost reinicializce (presneji, kam postavit detekcni miny pro reinicializaci). A protoze stale nejde poznat, co to tedy je, tak vysvetlim jak je to implementovane - prisnost znaci procentualni vzdalenost min od kraje. Tzn. ze 50% znamena, ze uz bude jen velice malo min na krajich. Nejdrive se podivame na chybu. Pro presnost podotykam, ze krok je 0.01, kde plna domena dosahuje chyby 9.05e-5 za XXX vterin (simulace probehly na starem clusteru).
Chyba
<3aniz7>
| Prisnost \ Sirka pasu v bodech |
20 |
30 |
40 |
50 |
60 |
70 |
| 10% |
||||||
| 20% |
1.24e-1 |
2.67e-2 |
2.85e-3 |
4.14e-3 |
||
| 30% |
1.06e-1 |
5.81e-2 |
2.23e-2 |
1.96e-3 |
||
| 40% |
6.49e-2 |
6.18e-2 |
4.36e-2 |
2.53e-2 |
||
| 50% |
4.88e-2 |
5.89e-2 |
4.61e-2 |
2.96e-2 |
Doba vypoctu/ / pocet reinicializaci
<3aniz7>
| Prisnost \ Sirka pasu v bodech |
20 |
30 |
40 |
50 |
60 |
70 |
| 10% |
||||||
| 20% |
5345 / 126 |
7179
/ 40 |
9676 / 24 |
12946
/ 17 |
||
| 30% |
4890 / 70 |
6737
/ 20 |
9418 / 13 |
12702
/ 10 |
||
| 40% |
4517 / 43 |
6602
/ 17 |
9325 / 10 |
12635
/ 7 |
||
| 50% |
4436 / 38 |
6595
/ 14 |
9319 / 9 |
12632
/ 6 |
A nakonec jen napocitani ucinnosti paralelizace na plne domene na SP. Na kroku 0.01 a casovem 7.8e-6.
<3aniz8>
| Pocet procesu |
1 |
4 |
8 |
12 |
16 |
| Doba vypoctu |
<NA> |
69423 |
35484 |
24038 |
18289 |
| LZV 1 |
- |
- |
102% |
104% |
105% |
| LZV predchozimu |
- |
- |
102% |
102% |
101% |
Bohuzel na jednom uzlu uz to nebylo mozne spocitat z duvodu omezeni doby vypoctu na 2dny. :-(
Ponekud zarazejici vysledek si vysvetluji tim, ze jsou to vsechno dualni masiny, kazde dva procesy tedy maji jen jeden komunikacni kanal. Dusledkem je, ze komunikace s ostatnimi procesy trva zhruba 2x tak dlouho, nez by melo - coz jsme presne pozorovali.