Lineární algebra srozumitelně

Soustavy lineárních algebraických rovnic

Úvod: Historie lineární algebry je otočená "nohama vzhůru". Odvíjela se totiž v opačném pořadí, než jak se dnes běžně vyučuje v prvním ročníku vysokých škol technického směru. Paradoxně se tedy nejprve objevily determinanty, až po nich matice a teprve začátkem 20. století se začal prosazovat pojem vektorový prostor. Úplně na začátku všeho stály a celým vývojem prostupovaly soustavy lineárních algebraických rovnic. Vždyť také algebra má původ ve slově al-jabr, které použil jako první v 9. století arabský matematik Al-Khwarizmi pro označení "sečtení 2 rovnic s cílem zbavit se neznámé".

Soustava lineárních algebraických rovnic: Prozraďme nyní, co je to soustava LAR. Nechť je dáno $m\cdot n$ koeficientů $a_{ij}$ a $m$ koeficientů pravé strany $b_i$. My budeme uvažovat ve valné většině úloh koeficienty reálné, ale samozřejmě v historii vždy počtáři pracovali s takovými čísly, která znali. Nejprve s přirozenými, poté racionálními kladnými a zápornými celými čísly, nakonec s reálnými a komplexními a dnes umíme pracovat i s koeficienty ještě obecnějšími, což ale v tuto chvíli není předmětem našeho zájmu. Řešit soustavu $m$ lineárních algebraických rovnic o $n$ neznámých znamená najít reálnou $n$-tici čísel ($x_1, x_2, \dots, x_n$), která vyhovují následujícím rovnicím.

$$\begin{matrix} a_{11}x_1&+&a_{12}x_2&+&\dots&+&a_{1n}x_n&=&b_1\\ a_{21}x_1&+&a_{22}x_2&+&\dots&+&a_{2n}x_n&=&b_2\\ &&&&\dots&&&&\\ a_{m1}x_1&+&a_{m2}x_2&+&\dots&+&a_{mn}x_n&=&b_m\\ \end{matrix}$$

Termín lineární souvisí s tím, že se neznámé $x_i$ vyskytují v první mocnině, tedy pouze jako $x_i^1$.
Velmi užitečné jsou pojmy matice soustavy a rozšířená matice soustavy. Získáme je tak, že koeficienty sestavíme do tabulek následujícím způsobem.

Takto vypadají matice soustavy $\mathbb A$ $$ \mathbb A= \left(\begin{matrix} a_{11}&a_{12}&\dots &a_{1n}\\ a_{21}&a_{22}&\dots &a_{2n}\\ \dots&\dots&\dots&\dots \\ a_{m1}&a_{m2}&\dots &a_{mn}\\ \end{matrix}\right)$$ a rozšířená matice soustavy $(\mathbb A|\vec b)$ $$(\mathbb A|\vec b)=\left(\begin{matrix} a_{11}&a_{12}&\dots &a_{1n}&b_1\\ a_{21}&a_{22}&\dots &a_{2n}&b_2\\ \dots&\dots&\dots&\dots&\dots \\ a_{m1}&a_{m2}&\dots &a_{mn}&b_m\\ \end{matrix}\right)$$

Ukažme si konkrétní příklad takové soustavy a najděme rovnou i její řešení. Nechť je dána soustava $$\begin{matrix} 3x&+&2y&+&4z&=&1\\ 2x&-&y&+&z&=&2\\ x&+&y&+&2z&=&0 \end{matrix}$$ Zřejmě téměř každého, kdo vidí takovou soustavu poprvé, napadne hledat řešení jedním z následujících dvou způsobů (stejnými myšlenkami, ale možná s jiným pořadím úprav).

• Vyjádříme z poslední rovnice $x$ a v první a druhé rovnici $x$ tímto vyjádřením $x=-y-2z$ nahradíme, $$\begin{matrix} 3(-y-2z)&+&2y&+&4z&=&1\\ 2(-y-2z)&-&y&+&z&=&2 \end{matrix}$$ Odtud dostaneme soustavu, která má jistě stejné řešení jako původní, a to $$\begin{matrix} x&=&-y&-&2z \\ -y&-&2z&=&1\\ -3y&-&3z&=&2 \end{matrix}$$ Nyní se soustřeďme na rovnice, které $x$ neobsahují. Z první z nich vyjádříme $y$ a toto vyjádření do druhé z nich dosadíme $y=-2z-1$ $$\begin{matrix} -3(-2z-1)&-&3z&=&2 \end{matrix}$$

Odtud dostaneme opět soustavu, která má jistě stejné řešení jako původní, a to $$\begin{matrix} x&=&-y&-&2z \\ y&=&-&2z&-&1\\ 3z&=&-1 \end{matrix}$$ Nyní již snadno řešení vyčteme. Z poslední rovnice máme $z=-\frac{1}{3}$, to dosadíme do předposlední a dostaneme $y=-\frac{1}{3}$ a nakonec dosadíme do první a máme $x=1$. Tedy $(1, -\frac{1}{3}, -\frac{1}{3})$ je hledané řešení. Z našeho postupu také vidíme, že soustava více řešení nemá.

Můžeme také eliminovat neznámé pomocí sčítání či odečítání rovnic. Uveďme úpravy, které jistě nebudou měnit množinu řešení:

• záměna pořadí rovnic,
• vynásobení rovnice nenulovým číslem,
• přičtení či odečtení násobku jiné rovnice od rovnice vybrané.

Teď takové úpravy použijeme (budeme je značit $\sim$) s cílem převést naši soustavu na jinou, která bude v poslední rovnici obsahovat jen neznámou $z$ a v předposlední jen neznámé $y$ a $z$. $$\begin{matrix} x&+&y&+&2z&=&0 \\ 3x&+&2y&+&4z&=&1\\ 2x&-&y&+&z&=&2 \end{matrix}$$ $$\sim \quad \begin{matrix} x&+&y&+&2z&=&0 \\ &-&y&-&2z&=&1\\ &-&3y&-&3z&=&2 \end{matrix} $$ $$\sim \quad \begin{matrix} x&+&y&+&2z&=&0 \\ &-&y&-&2z&=&1\\ &&&&3z&=&-1 \end{matrix}$$ V prvním kroku jsme zaměnili pořadí rovnic, ve 2. kroku jsme od druhé rovnice odečetli 3-násobek první a od třetí rovnice jsme odečetli 2-násobek první. Tím jsme se ve druhé a třetí rovnici zbavili neznámé $x$. Ve 3. kroku jsme od poslední rovnice odečetli 3-násobek druhé, tím jsme se zbavili neznámé $y$ a získali jsme kýžený tvar, z nějž snadno vyčteme řešení $(1, -\frac{1}{3}, -\frac{1}{3})$. Opět vidíme, že jiné řešení soustava nemá. Rozmyslete si, že obě metody jsou vlastně převlečená jedna a ta samá!

Zde je program, který metodami analogickými předchozímu příkladu hledá řešení jakékoliv soustavy 3 rovnic pro 3 neznámé, ovšem za podmínky, že tato soustava má řešení jediné.

Dávná historie: Egypťané a Babyloňané již před 4000 lety řeší soustavy 2 LAR o 2 neznámých. Takové úlohy zapisují pouze slovně, vždy řeší soustavy s konkrétními číselnými koeficienty, které mají původ v praktických úlohách (Egypťané počítají měřice ječmene a Babylonci gury obilí). Koeficienty jsou jen přirozená čísla a jako výsledek připouští i jednoduché zlomky.

150 - 50 př. n. l. Číňané v 8. kapitole Devíti traktátů o matematickém umění (také se někdy říká Matematika v devíti kapitolách) řeší 18 slovních úloh vedoucích na soustavy LAR, používají metodu fang čcheng, která je předchůdkyní Gaussova eliminačního algoritmu a používá sloupcové úpravy. Čínští počtáři umí pracovat s přirozenými čísly a jednoduchými zlomky, ale v mezivýpočtech připouští i čísla záporná, definují základní aritmetické operace s takovými čísly, ale barví je červenou tuší a nepovažují je ještě za plnohodnotná čísla.

Japonec Takakazu Šinsuke Seki Kowa (1642-1708) a jeho žáci rozvíjí metodu fang čcheng a jejím prostřednictvím dospívají k pojmu determinant. Seki Kowa (na obrázku) bývá občas považován za objevitele determinantu.

Staří Řekové, ač jsou považováni za zakladatele opravdové matematiky (stojí u zrodu toho nejdůležitějšího v celé matematice - nutnosti tvrzení dokázat), k rozvoji řešení soustav LAR významně nepřispěli. Jedním z důvodů byla zřejmě jejich složitá číselná soustava, v níž se aritmetické výpočty prováděli obtížně, druhým pak jejich zájem zaostřený na geometrii. Právě kvůli geometrii pracují jen s kladnými zpočátku pouze racionálními čísly (záporná čísla nemohou představovat délku úsečky či obsah nějakého útvaru).

Teprve indický učenec Brahmagupta přichází v 7. stol. s definicí nuly jakožto čísla (poziční nula, která značí prázdné místo v zápisu čísel v pozičních číselných soustavách, má kořeny již ve staré Babylonii). Brahmagupta definuje operace s nulou a se zápornými čísly (představuje si je jako dluh). Od této chvíle se koeficienty i výsledky v soustavách LAR mohou pohybovat i v oblasti záporných čísel. Další indickou zajímavostí je, že neznámým dávají jména barev. Do středověké Evropy se indické poznatky dostávají prostřednictvím Arabů.

Do 17. století: V 16. stol. se začíná vytvářet algebraická symbolika. François Viète v Analytickém umění značí neznámé samohláskami a koeficienty souhláskami a užívá dnešní znaky pro plus a mínus +,-. Navíc jako první vyjadřuje tvar řešení soustavy v závislosti na koeficientech - i slovo koeficient je od něj. Dnešní značení se poprvé objevuje u Reného Descarta: koeficienty značí $a, b, c, \dots$ neznámé $x, y, z,\dots $ a soustavu zapisuje tak, že je na pravé straně každé rovnice nula.

Determinant: Ukažme si nejprve, jak spočíst determinant matice rozměru $2 \times 2$ a $3 \times 3$ (matici si představujme jako tabulku čísel). K tomu se hodí oblíbené Sarrusovo pravidlo, které ilustruje obrázek s modrými a červenými šipkami. Jak uvidíme dále, pro zápis determinantu matice $\mathbb A$ se používá $\text{det}({\mathbb A})$ nebo se matice píše mezi svislé čáry.

Chceme-li vypočítat determinant matice $\mathbb A=\left(\begin{matrix}1 &0&1\\ 1&2&0\\ 2&1&3\end{matrix} \right),$ bereme součiny prvků spojených modrými šipkami se znaménkem plus a součiny prvků spojených červenými šipkami se znaménkem mínus. $$\left|\begin{matrix}1 &0&1\\ 1&2&0\\ 2&1&3\end{matrix} \right|=$$ $$=1\cdot 2\cdot 3+1\cdot 1\cdot 1+2\cdot 0\cdot 0-2\cdot 2\cdot 1-1\cdot 1\cdot 0-1\cdot 0\cdot 3=3.$$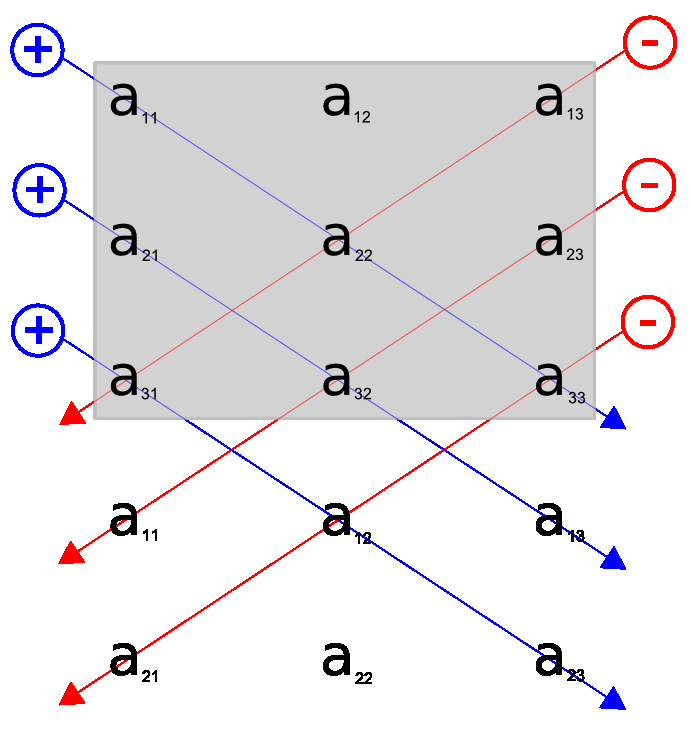

Za objevitele determinantu bývá obvykle považován Gottfried Wilhelm Leibniz (1646 Lipsko - 1716 Hannover). V roce 1693 píše dopis markýzi L’Hospitalovi, ve kterém tvrdí, že pokud soustava $n + 1$ LAR o $n$ neznámých s pravou stranou má řešení, pak je nutně determinant rozšířené matice soustavy nulový. Nepoužívá ještě ovšem slovo determinant, protože takové označení použije poprvé až Gauss, a samozřejmě ani matice, poněvadž s tím přijde ještě o něco později Sylvester. Leibniz v dopise chválí své novátorské značení: $ij$ pro koeficient $a_{ij}$ a $i0$ pro $i$-tou složku pravé strany $b_i$. Soustava $3\times 3$ při použití Leibnizova značení vypadá následovně: $$\begin{matrix}10 &+& 11x &+& 12y &+& 13z &=& 0\\ 20 &+& 21x &+& 22y &+& 23z &=& 0\\ 30 &+& 31x &+& 32y &+& 33z &=& 0 \end{matrix}$$ Popis vytváření determinantu je nepraktický, a tak jeho nápad zůstává bez ohlasu.

Determinanty se dostávají do centra pozornosti matematiků přesně v polovině 18. století. V roce 1750 publikuje švýcarský matematik Gabriel Cramer Introduction à l'analyse des lignes courbes algébriques (Úvod do analýzy algebraických křivek). Cramera vedl k řešení soustav problém nalezení kuželosečky procházející konkrétními 5 body v rovině. Připomeňme, že rovinná kuželosečka je množina bodů $(x,y)$, které splňují rovnici $x^2 + Ay^2 + Bxy + Cx + Dy + E = 0$. Jistě příklady takových kuželoseček znáte:

• kružnice $x^2+y^2-1=0$
• elipsa $\frac{x^2}{2}+y^2-1=0$
• hyperbola $x^2-y^2-1=0$
• parabola $x^2 - y = 0$

Po dosazení 5 bodů do rovnice kuželosečky získáme soustavu 5 rovnic pro 5 neznámých $A, B, C, D, E$. Cramer v dodatku svého díla vysvětluje, jak soustavu LAR $n \times n$ řešit, a to i pro $n>5$. Důkazy svých tvrzení ovšem uvádí jen pro soustavy rozměru $2\times 2$ a $3\times 3$.