Rychlé násobení
je násobení se složitostí menší než násobení klasické. Snaha o zrychlení algoritmů se zesiluje ruku v ruce s rozvojem počítačů a speciálně snaha o maximální zrychlení násobení je dána potřebami kryptografie, kde je nutné násobit v přijatelném čase ohromná čísla (řádově 10100).
My popíšeme dvě rychlá násobení - Karacubovo násobení a Schönhageovo násobení v modulární aritmetice - založená na důvtipných myšlenkách a poměrně jednoduše popsatelná. Mezi rychlými algoritmy patří k těm nejstarším, ovšem algoritmy ještě rychlejší už jsou příliš technické.
Zájemce o násobení přirozených čísel s binárním rozvojem délky n blížící se svou složitostí libovolně blízko až k nejnižší hranici O(n) si dohledá podrobnosti v D. E. Knuth, The Art of Computer Programming volume 2: Seminumerical Algorithms, 3rd ed, Addison-Wesley Boston etc., 1998.
Poznamenejme, že jde o jednu z nejrespektovanějších publikací v oboru programování. Donald E. Knuth (na obrázku) je průkopníkem oboru matematické algoritmické analýzy a významnou osobností v mnoha dalších oborech teoretické počítačové vědy.
Karacubovo násobení
Karacubovo násobení vyvrátilo domněnku, že složitost násobení dvou přirozených čísel s binárním rozvojem délky n je O(n2). Tento názor razil ještě v roce 1960 na semináři moskevské univerzity zakladatel teorie složitosti algoritmů Andrej N. Kolmogorov (na obrázku).
Semináře se účastnil jeho student Anatolij A. Karacuba, který navrhl a o dva roky později publikoval důvtipný algoritmus s nižší složitostí. Popíšeme algoritmus, který je založen na stejné myšlence jako původní Karacubův, ale je ještě trochu jednodušší.
Chceme násobit dvě 2n-bitová čísla
U s binárním zápisem u2n-1...u1u0 a V s binárním zápisem v2n-1...v1v0.
 Není těžké dokázat, že složitost Karacubova násobení je O(nlog23). Platí log23 je přibližně 1,585, což je číslo menší než 2, a tedy jde skutečně o rychlé násobení podle naší definice.
Není těžké dokázat, že složitost Karacubova násobení je O(nlog23). Platí log23 je přibližně 1,585, což je číslo menší než 2, a tedy jde skutečně o rychlé násobení podle naší definice.
Adaptací na desítkovou soustavu lze převést násobení 8-místných čísel na násobení čísel 4-místných, které už dobří počtáři zvládnou zpaměti. Kupodivu se nezdá, že by taková metoda byla známa před rokem 1962 a že by ji tedy používali "zázrační počtáři", kteří v minulosti bavili obecenstvo násobením obrovských čísel zpaměti.
Schönhageovo násobení v modulární aritmetice
Schönhageovo násobení v modulární aritmetice sice není rychlejší než Karacubův algoritmus, ale je založeno na odlišných myšlenkách a na neobvyklé reprezentaci čísel, takže je rozhodně zajímavé do jeho tajů proniknout.
Jeho základním stavebním kamenem je modulární aritmetika, u jejíhož zrodu stáli čeští vědci Antonín Svoboda (tvůrce prvního československého počítače SAPO a velmi významný průkopník informatiky nejen u nás - o jeho klikatých osudech se dočtete v článku Petra Vysokého 100 let od narození Antonína Svobody a jeho podobu vidíte na obrázku) a Miroslav Valach. Nezávisle na nich přišel se stejnou myšlenkou také L. H. Garner.
Modulární zápis
Dosud jsme se seznámili jen se zápisy přirozených čísel v pozičních soustavách s přirozenou bází (případně jsme připustili záporné cifry). Nyní přijde naprosto odlišný zápis přirozených čísel.
Nechť jsou dána přirozená čísla m1, m2, ..., mr. Pak modulárním zápisem nezáporného celého čísla U nazveme (u1,u2,...,ur,), kde ui je rovno U mod mi pro každé i od 1 do r. Připomeňme, že mod k znamená zbytek po celočíselném dělení číslem k a nabývá hodnot od 0 do k-1. (Například 13=3.4+1, a tedy 13 mod 4=1.) Ukažme si na příkladu takovou modulární reprezentaci.
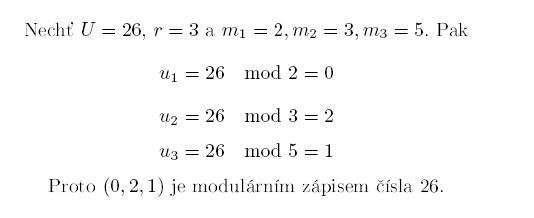 Aby takový zápis měl smysl, mělo by být možné původní číslo ze znalosti modulární reprezentace zrekonstruovat. To bez dodatečných podmínek možné není. Všimněme si, že čísla 56 a 26 mají stejný modulární zápis (0,2,1).
Naštěstí platí následující tvrzení, které je důsledkem známé Čínské zbytkové věty:
Aby takový zápis měl smysl, mělo by být možné původní číslo ze znalosti modulární reprezentace zrekonstruovat. To bez dodatečných podmínek možné není. Všimněme si, že čísla 56 a 26 mají stejný modulární zápis (0,2,1).
Naštěstí platí následující tvrzení, které je důsledkem známé Čínské zbytkové věty:
Nechť a,u1,u2,...,ur jsou nezáporná celá čísla a nechť m1, m2, ..., mr jsou přirozená po dvou nesoudělná čísla. Pak existuje právě jedno U, které splňuje
Modulární aritmetika
V modulární aritmetice je možné paralelizovat sčítání a násobení. Platí totiž, že pokud U a V jsou přirozená čísla s modulárními reprezentacemi (u1,u2,...,ur) a (v1,v2,...,vr) a obě leží mezi 0 a m = m1. m2. ... . mr, pak
Binární modulární aritmetika
Jak uvidíme, takovou rychlou konverzi poskytuje vhodná volba modulí m1, m2, ..., mr. Následující nápad se zrodil v hlavě A. S. Fraenkela.
Volme modula mi= 2ei -1, kde e1 < e2 < ... < er jsou po dvou nesoudělná. Nesoudělnost takových modulí je zaručena následující větou:
Nechť e, f jsou přirozená čísla. Pak 2e -1 a 2f -1 jsou nesoudělná, právě když e a f jsou nesoudělná
Konverze U na (u1,u2,...,ur)
Zapišme U ve tvaru U = atAt + at-1At-1 + ... +a1A + a0, kde A = 2ei. Uvědomme si, že binární zápis a0 získáme tak, že vezmeme posledních ei bitů v binárním zápisu U, pro získání a1 vezmeme předposledních ei bitů atd. Vlastně jen nasekáme binární zápis U od konce po ei bitech. Protože A = 1 mod (2ei-1), dostaneme ui = (at + at-1 + ... + a0) mod (2ei-1).
V desítkové soustavě máme analogii (tzv. casting out nines - vyloučení devítek)
789 mod 9 = 7 + 8 + 9 mod 9 = 6, což skutečně platí, protože 789 = 87.9 + 6. Ilustrujme tento algoritmus opět na příkladu.

Konverze (u1,u2,...,ur) na U
Je o něco složitější. Probíhá ve dvou krocích:
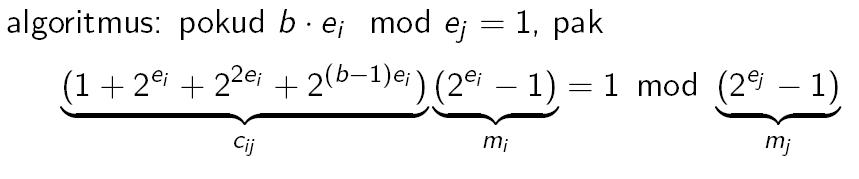

Schönhageovo násobení
Nyní máme vše připraveno k tomu, abychom pochopili fungování algoritmu, který Arnold Schönhage v roce 1966 navrhl. Nejprve si všimněme, jak šikovně volí 6 modulí, která budou v jeho algoritmu vystupovat.
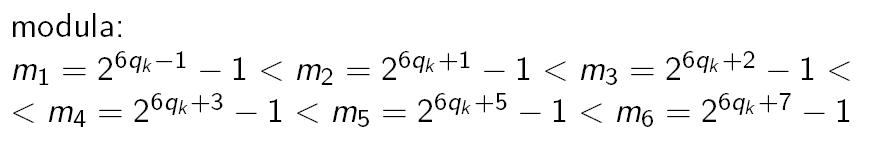 Pro posloupnost q0=1 a qk=3qk-1-1,
tj. qk=(3k+1)/2 pro každé k přirozené, jsou modula po dvou nesoudělná.
Navíc platí, že při násobení pk=(18qk+8)-bitových čísel nedojde k přetečení,
tj. zůstaneme mezi 0 a m=m1. m2. ... . m6,
protože m je větší než 22pk.
Pro posloupnost q0=1 a qk=3qk-1-1,
tj. qk=(3k+1)/2 pro každé k přirozené, jsou modula po dvou nesoudělná.
Navíc platí, že při násobení pk=(18qk+8)-bitových čísel nedojde k přetečení,
tj. zůstaneme mezi 0 a m=m1. m2. ... . m6,
protože m je větší než 22pk.
Teď již samotný Schönhageův algoritmus. Chceme násobit přirozená čísla U a V, označme W = U x V. Najdeme nejmenší pk tak, že násobená čísla jsou nejvýše pk-bitová. K pk najdeme příslušná modula.
 Tento algoritmus převádí úlohu násobit pk-bitová čísla na násobení pk-1-bitových čísel.
To je podobná myšlenka jako v Karacubově násobení vedoucí ke snížení složitosti.
Tentokrát je možné - i když pracné - dokázat, že složitost Schönhageova násobení je O(nlog36).
Platí log36 je přibližně 1,63, což je číslo menší než 2, a tedy jde opět o rychlé násobení podle naší definice.
Tento algoritmus převádí úlohu násobit pk-bitová čísla na násobení pk-1-bitových čísel.
To je podobná myšlenka jako v Karacubově násobení vedoucí ke snížení složitosti.
Tentokrát je možné - i když pracné - dokázat, že složitost Schönhageova násobení je O(nlog36).
Platí log36 je přibližně 1,63, což je číslo menší než 2, a tedy jde opět o rychlé násobení podle naší definice.
 |
Karacubovo násobení vyvrátilo domněnku, že složitost násobení dvou přirozených čísel s binárním rozvojem délky n je O(n2). Tento názor razil ještě v roce 1960 na semináři moskevské univerzity zakladatel teorie složitosti algoritmů Andrej N. Kolmogorov (na obrázku).
 |
- Zapíšeme U, V následujícím způsobem U = 2nU1 + U0 a V = 2nV1 + V0. Platí tedy, že U1 má binární zápis u2n-1...un a U0 má zápis un-1...u1u0, podobně V1 má binární zápis v2n-1...vn a V0 má zápis vn-1...v1v0.
- Následující formule redukuje problém na 3 násobení n-bitových čísel, několik sčítání, resp. odečítání a posouvání binární čárky:
U×V = (22n+2n)U1V1+2n(U1-U0)(V0-V1)+(2n+1)U0V0.

Adaptací na desítkovou soustavu lze převést násobení 8-místných čísel na násobení čísel 4-místných, které už dobří počtáři zvládnou zpaměti. Kupodivu se nezdá, že by taková metoda byla známa před rokem 1962 a že by ji tedy používali "zázrační počtáři", kteří v minulosti bavili obecenstvo násobením obrovských čísel zpaměti.
Schönhageovo násobení v modulární aritmetice
Schönhageovo násobení v modulární aritmetice sice není rychlejší než Karacubův algoritmus, ale je založeno na odlišných myšlenkách a na neobvyklé reprezentaci čísel, takže je rozhodně zajímavé do jeho tajů proniknout.
 |
Modulární zápis
Dosud jsme se seznámili jen se zápisy přirozených čísel v pozičních soustavách s přirozenou bází (případně jsme připustili záporné cifry). Nyní přijde naprosto odlišný zápis přirozených čísel.
Nechť jsou dána přirozená čísla m1, m2, ..., mr. Pak modulárním zápisem nezáporného celého čísla U nazveme (u1,u2,...,ur,), kde ui je rovno U mod mi pro každé i od 1 do r. Připomeňme, že mod k znamená zbytek po celočíselném dělení číslem k a nabývá hodnot od 0 do k-1. (Například 13=3.4+1, a tedy 13 mod 4=1.) Ukažme si na příkladu takovou modulární reprezentaci.
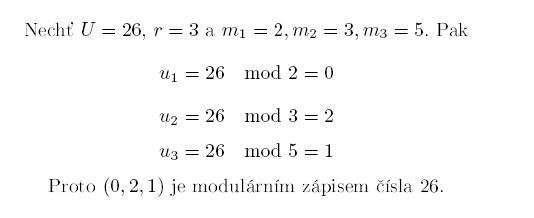
Nechť a,u1,u2,...,ur jsou nezáporná celá čísla a nechť m1, m2, ..., mr jsou přirozená po dvou nesoudělná čísla. Pak existuje právě jedno U, které splňuje
- a - 1 < U < a + m = a + m1. m2. ... . mr,
- (u1,u2,,...,ur) je modulární reprezentace U.
Modulární aritmetika
V modulární aritmetice je možné paralelizovat sčítání a násobení. Platí totiž, že pokud U a V jsou přirozená čísla s modulárními reprezentacemi (u1,u2,...,ur) a (v1,v2,...,vr) a obě leží mezi 0 a m = m1. m2. ... . mr, pak
- U + V má modulární reprezentaci ((u1+v1) mod m1, (u2+v2) mod m2,...,(ur+vr) mod mr),
- U x V má modulární reprezentaci ((u1.v1) mod m1, (u2.v2) mod m2,...,(ur.vr) mod mr).
Binární modulární aritmetika
Jak uvidíme, takovou rychlou konverzi poskytuje vhodná volba modulí m1, m2, ..., mr. Následující nápad se zrodil v hlavě A. S. Fraenkela.
Volme modula mi= 2ei -1, kde e1 < e2 < ... < er jsou po dvou nesoudělná. Nesoudělnost takových modulí je zaručena následující větou:
Nechť e, f jsou přirozená čísla. Pak 2e -1 a 2f -1 jsou nesoudělná, právě když e a f jsou nesoudělná
Konverze U na (u1,u2,...,ur)
Zapišme U ve tvaru U = atAt + at-1At-1 + ... +a1A + a0, kde A = 2ei. Uvědomme si, že binární zápis a0 získáme tak, že vezmeme posledních ei bitů v binárním zápisu U, pro získání a1 vezmeme předposledních ei bitů atd. Vlastně jen nasekáme binární zápis U od konce po ei bitech. Protože A = 1 mod (2ei-1), dostaneme ui = (at + at-1 + ... + a0) mod (2ei-1).
V desítkové soustavě máme analogii (tzv. casting out nines - vyloučení devítek)
789 mod 9 = 7 + 8 + 9 mod 9 = 6, což skutečně platí, protože 789 = 87.9 + 6. Ilustrujme tento algoritmus opět na příkladu.

Konverze (u1,u2,...,ur) na U
Je o něco složitější. Probíhá ve dvou krocích:
- Nejprve je třeba najít r(r-1)/2 konstant cij, indexy i,j nabývají hodnot od 1 do r, i < j a platí
cijmi=1 mod mj.
K tomu využijeme následující algoritmus.
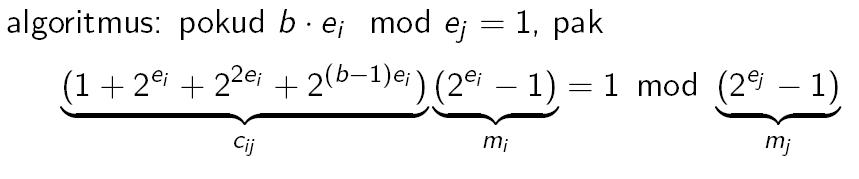
- Poté položíme U = vr mr-1...m2m1 +...+ v3 m2m1 + v2 m1 + v1, kde
v1 = u1 mod m1
v2 = (u2-v1)c12 mod m2
v3 = ((u3-v1)c13-v2)c23 mod m3
...
vr = (((ur-v1)c1r-v2)c2r-...)cr-1r mod mr
Snadno se přesvědčíme, že takto spočtené U splňuje- U je nezáporné číslo menší než m,
- U mod mi = ui pro každé i od 1 do r.

Schönhageovo násobení
Nyní máme vše připraveno k tomu, abychom pochopili fungování algoritmu, který Arnold Schönhage v roce 1966 navrhl. Nejprve si všimněme, jak šikovně volí 6 modulí, která budou v jeho algoritmu vystupovat.
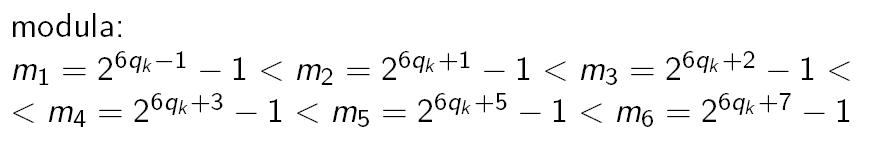
Teď již samotný Schönhageův algoritmus. Chceme násobit přirozená čísla U a V, označme W = U x V. Najdeme nejmenší pk tak, že násobená čísla jsou nejvýše pk-bitová. K pk najdeme příslušná modula.

Aritmetika včera a dnes
Rychlé násobení
Úvod
Násobení
Násobení na prstech
Násobení na papíře
Mechanické pomůcky a tabulky
Počítačové násobení
Dělení
Dělení na papíře
Mechanické pomůcky
Odmocnina
Sčítání
Starověké kultury
Významní matematikové
Aplikace na android ke stažení na Google Play 